Uniform distribution

A continuous random variable has a uniform distribution if all the values belonging to its support have the same probability density.

Table of contents

Definition
Expected value
Variance
Moment generating function
Characteristic function
Distribution function
Density plots
1. Plot 1 - Different supports but same length
2. Plot 2 - Different supports and different lengths
Solved exercises

Definition

The uniform distribution is characterized as follows.

Definition Let be a continuous random variable. Let its support be a closed interval of real numbers:We say that has a uniform distribution on the interval if and only if its probability density function is [eq2]

A random variable having a uniform distribution is also called a uniform random variable. Sometimes, we also say that it has a rectangular distribution or that it is a rectangular random variable.

To better understand the uniform distribution, you can have a look at its density plots.

Expected value

The expected value of a uniform random variable is

Proof

It can be derived as follows: [eq4]

Variance

The variance of a uniform random variable is [eq5]

Proof

We can use the variance formula as follows: [eq7]

Moment generating function

The moment generating function of a uniform random variable is defined for any : [eq8]

Proof

Using the definition of moment generating function, we get [eq9] Note that the above derivation is valid only when . However, when :Furthermore, it is easy to verify thatWhen , the integral above is well-defined and finite for any . Thus, the moment generating function of a uniform random variable exists for any .

Characteristic function

The characteristic function of a uniform random variable is [eq12]

Proof

Using the definition of characteristic function, we obtain [eq13] Note that the above derivation is valid only when . However, when :Furthermore, it is easy to verify that

Distribution function

The distribution function of a uniform random variable is [eq16]

Proof

If , thenbecause can not take on values smaller than . If , then [eq18] If , thenbecause can not take on values greater than .

Density plots

This section shows the plots of the densities of some uniform random variables, in order to demonstrate how the uniform density changes by changing its parameters.

Plot 1 - Different supports but same length

The following plot contains the graphs of two uniform probability density functions:

the first graph (red line) is the probability density function of a uniform random variable with support ;
the second graph (blue line) is the probability density function of a uniform random variable with support .

The two random variables have different supports, but their two supports have the same length. Therefore, since the uniform density is constant and inversely proportional to the length of the support, the two random variables have the same constant density over their respective supports.

Plot 2 - Different supports and different lengths

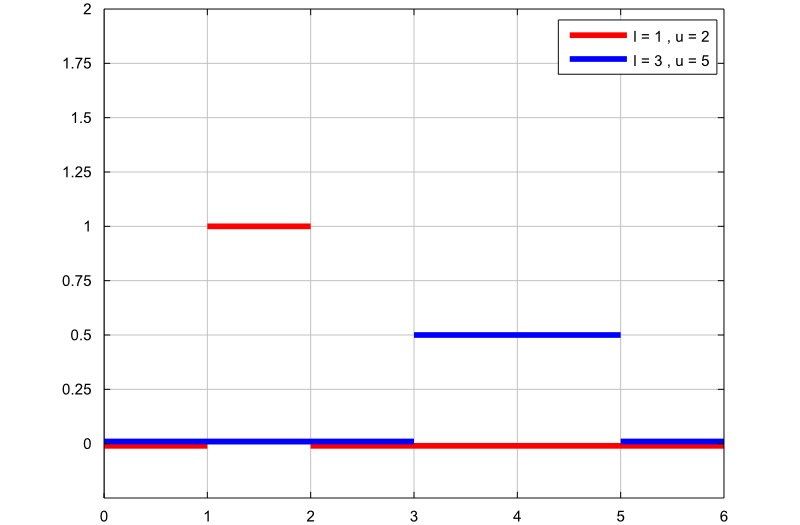
The following plot contains the graphs of two uniform probability density functions:

the first graph (red line) is the probability density function of a uniform random variable with support ;
the second graph (blue line) is the probability density function of a uniform random variable with support .

The two random variables have different supports, and the length of $R_{Y}$ is twice the length of . Therefore, since the uniform density is constant and inversely proportional to the length of the support, the second random variable has a constant density which is half the constant density of the first one.

Solved exercises

Below you can find some exercises with explained solutions.

Exercise 1

Let be a uniform random variable with support Compute the following probability:

Solution

We can compute this probability by using the probability density function or the distribution function of . Using the probability density function, we obtain [eq26] Using the distribution function, we obtain [eq27]

Exercise 2

Suppose the random variable has a uniform distribution on the interval . Compute the following probability:

Solution

This probability can be easily computed by using the distribution function of : [eq30]

Exercise 3

Suppose the random variable has a uniform distribution on the interval . Compute the third moment of , that is,

Solution

We can compute the third moment of by using the transformation theorem: [eq32]

How to cite

Please cite as:

Taboga, Marco (2021). "Uniform distribution", Lectures on probability theory and mathematical statistics. Kindle Direct Publishing. Online appendix. https://www.statlect.com/probability-distributions/uniform-distribution.