Independent events

Two events are said to be independent if the occurrence of one of them makes it neither more nor less probable that the other occurs.

Table of contents

Definition using conditional probabilities
Standard definition
Example
How to check independence
Mutually independent events
Zero-probability events and independence
Solved exercises

Definition using conditional probabilities

Let and be two events.

After receiving the information that will happen, we revise our assessment of the probability that will happen, by computing the conditional probability of given .

The events and are said to be independent if the probability of remains the same as it was before receiving the information:and, conversely,

Standard definition

In standard probability theory, rather than characterizing independence by properties (1) and (2) above, we define it in a more compact way, as follows.

Definition Two events and are said to be independent events if and only if

It is easy to prove that this definition implies properties (1) and (2) above.

Proof

Suppose and are independent and . Then, [eq5] Note that we have assumed . When , things are more complicated (see the discussion about division by zero in the lecture on conditional probability and in the references therein). It is exactly because of the difficulties that arise in defining when that a general definition of independence is not given by using properties (1) and (2).

Example

The following example shows how to check whether two events are independent in a simple probabilistic experiment.

Example An urn contains four balls $B_{1}$ , $B_{2}$ , $B_{3}$ and $B_{4}$ . We draw one of them at random. The sample space isEach of the four balls has the same probability of being drawn, equal to $frac{1}{4}$ , that is, [eq11] Define the events and as follows: [eq12] Their respective probabilities are [eq13] The probability of the event is [eq14] Hence, [eq15] As a consequence, and are independent events.

How to check independence

As shown in the previous example, the easiest way to check the independence of two events and is to verify that the standard definition applies:

compute the product of the probabilities of and ;
compute the probability of ;
if the two quantities computed in step 1 and 2 are equal, then the two events are independent.

However, one could also verify that condition (1) above holds because [eq16] or that condition (2) holds because [eq17]

The ways to check independence are summarized in the following infographic.

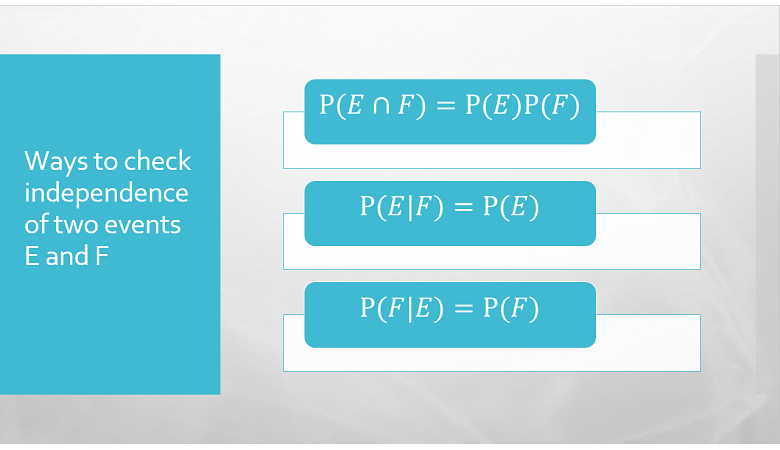
Infographic: there are three ways to check the independence of two events.

Mutually independent events

The definition of independence can be extended also to collections of more than two events.

Definition Let $E_{1}$ , ..., $E_{n}$ be events. $E_{1}$ , ..., $E_{n}$ are jointly independent (or mutually independent) if and only if for any sub-collection of events () $E_{i_{1}}$ , ..., $E_{i_{k}}$ : [eq18]

Let $E_{1}$ , ..., $E_{n}$ be a collection of events. It is important to note that even if all the possible couples of events are independent (i.e., $E_{i}$ is independent of $E_{j}$ for any ), this does not imply that the events $E_{1}$ , ..., $E_{n}$ are jointly independent. This is proved with a simple counter-example.

Example Consider the experiment presented in the previous example (extracting a ball from an urn that contains four balls). Define the events , and as follows: [eq19] It is immediate to show that [eq20] Thus, all the possible couple of events in the collection , , are independent. However, the three events are not jointly independent. In fact, [eq21]

On the contrary, it is obviously true that if $E_{1}$ , ..., $E_{n}$ are jointly independent, then $E_{i}$ is independent of $E_{j}$ for any .

Zero-probability events and independence

If is a zero-probability event, then is independent of any other event .

Proof

Note thatAs a consequence, by the monotonicity of probability,But , so . Since probabilities cannot be negative, it must be . The latter fact implies independence:

Solved exercises

Below you can find some exercises with explained solutions.

Exercise 1

Suppose that we toss a die. Six numbers (from to can appear face up, but we do not yet know which one of them will appear. The sample space isEach of the six numbers is a sample point and is assigned probability $frac{1}{6}$ . Define the events and as follows: [eq29] Prove that and are independent events.

Solution

The probability of is [eq30] The probability of is [eq31] The probability of is [eq32] and are independent events because

Exercise 2

A firm undertakes two projects, and . The probabilities of having a successful outcome are $frac{3}{4}$ for project and $frac{1}{2}$ for project . The probability that both projects will have a successful outcome is $frac{7}{16}$ . Are the two outcomes independent?

Solution

Denote by the event "project is successful", by the event "project is successful" and by the event "both projects are successful". The event can be expressed asIf and are independent, it must be that [eq35] Therefore, the two outcomes are not independent.

Exercise 3

A firm undertakes two projects, and . The probabilities of having a successful outcome are $frac{2}{3}$ for project and $frac{4}{5}$ for project . What is the probability that neither of the two projects will have a successful outcome if their outcomes are independent?

Solution

Denote by the event "project is successful", by the event "project is successful" and by the event "neither of the two projects is successful". The event can be expressed as:where $E^{c}$ and $F^{c}$ are the complements of and . Using De Morgan's law () and the formula for the probability of a complement, we obtain [eq38] By using the formula for the probability of a union, we obtain [eq39] Finally, since and are independent, we have that [eq40]

How to cite

Please cite as:

Taboga, Marco (2021). "Independent events", Lectures on probability theory and mathematical statistics. Kindle Direct Publishing. Online appendix. https://www.statlect.com/fundamentals-of-probability/independent-events.