Search for probability and statistics terms on Statlect
StatLect
Index > Probability distributions

Normal distribution

by , PhD

The normal distribution is a continuous probability distribution that plays a central role in probability theory and statistics.

It is often called Gaussian distribution, in honor of Carl Friedrich Gauss (1777-1855), an eminent German mathematician who gave important contributions towards a better understanding of the normal distribution.

Table of Contents

Why is it so important?

The normal distribution is extremely important because:

Main characteristics

Sometimes it is also referred to as "bell-shaped distribution" because the graph of its probability density function resembles the shape of a bell.

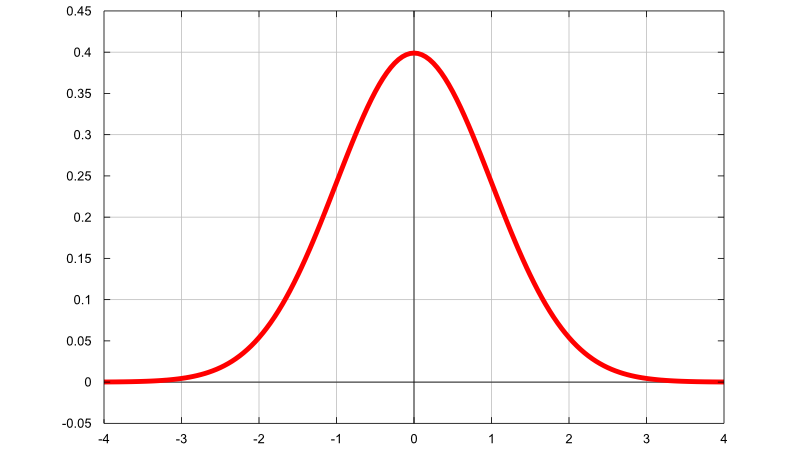
Plot of the normal density

As you can see from the above plot, the density of a normal distribution has two main characteristics:

The remainder of this lecture gives a formal presentation of the main characteristics of the normal distribution.

First, we deal with the special case in which the distribution has zero mean and unit variance. Then, we present the general case, in which mean and variance can take any value.

The standard normal distribution

The adjective "standard" indicates the special case in which the mean is equal to zero and the variance is equal to one.

Definition

Standard normal random variables are characterized as follows.

Definition Let X be a continuous random variable. Let its support be the whole set of real numbers:[eq1]We say that X has a standard normal distribution if and only if its probability density function is[eq2]

The following is a proof that [eq3] is indeed a legitimate probability density function:

Proof

The function [eq4] is a legitimate probability density function if it is non-negative and if its integral over the support equals 1. The former property is obvious, while the latter can be proved as follows:[eq5]

Expected value

The expected value of a standard normal random variable X is[eq6]

Proof

It can be derived as follows:[eq7]

Variance

The variance of a standard normal random variable X is[eq8]

Proof

It can be proved with the usual variance formula ([eq9]):[eq10]

Moment generating function

The moment generating function of a standard normal random variable X is defined for any t in R:[eq11]

Proof

It is derived by using the definition of moment generating function:[eq12]The integral above is well-defined and finite for any t in R. Thus, the moment generating function of X exists for any t in R.

Characteristic function

The characteristic function of a standard normal random variable X is[eq13]

Proof

By the definition of characteristic function, we have[eq14]Now, take the derivative with respect to $t$ of the characteristic function:[eq15]By putting together the previous two results, we obtain[eq16]The only function that satisfies this ordinary differential equation (subject to the condition [eq17]) is[eq18]

Distribution function

There is no simple formula for the distribution function [eq19] of a standard normal random variable X because the integral[eq20]cannot be expressed in terms of elementary functions. Therefore, it is usually necessary to resort to special tables or computer algorithms to compute the values of [eq21]. The lecture entitled Normal distribution values discusses these alternatives in detail.

The normal distribution in general

While in the previous section we restricted our attention to the special case of zero mean and unit variance, we now deal with the general case.

Definition

The normal distribution with mean mu and variance sigma^2 is characterized as follows.

Definition Let X be a continuous random variable. Let its support be the whole set of real numbers:[eq22]Let $mu in U{211d} $ and [eq23]. We say that X has a normal distribution with mean mu and variance sigma^2 if and only if its probability density function is[eq24]

We often indicate the fact that X has a normal distribution with mean mu and variance sigma^2 by[eq25]

To better understand how the shape of the distribution depends on its parameters, you can have a look at the density plots at the bottom of this page.

Relation between standard and non-standard normal distribution

The following proposition provides the link between the standard and the general case.

Proposition If X has a normal distribution with mean mu and variance sigma^2, then[eq26]where Z is a random variable having a standard normal distribution.

Proof

This can be easily proved using the formula for the density of a function of a continuous variable ([eq27] is a strictly increasing function of Z, since $sigma $ is strictly positive):[eq28]

Thus, a normal distribution is standard when $mu =0$ and $sigma ^{2}=1$.

Expected value

The expected value of a normal random variable X is[eq29]

Proof

The proof is a straightforward application of the fact that X can we written as a linear function of a standard normal variable:[eq30]

Variance

The variance of a normal random variable X is[eq31]

Proof

It can be derived as follows:[eq32]

Moment generating function

The moment generating function of a normal random variable X is defined for any t in R:[eq33]

Proof

The mgf is derived as follows:[eq34]It is defined for any t in R because the moment generating function of Z is defined for any t in R.

Characteristic function

The characteristic function of a normal random variable X is[eq35]

Proof

The derivation is similar to the derivation of the moment generating function:[eq36]

Distribution function

The distribution function [eq37] of a normal random variable X can be written as[eq38]where [eq39] is the distribution function of a standard normal random variable Z (see above). The lecture entitled Normal distribution values provides a proof of this formula and discusses it in detail.

Density plots

This section shows the plots of the densities of some normal random variables. These plots help us to understand how the shape of the distribution changes by changing its parameters.

Plot 1 - Changing the mean

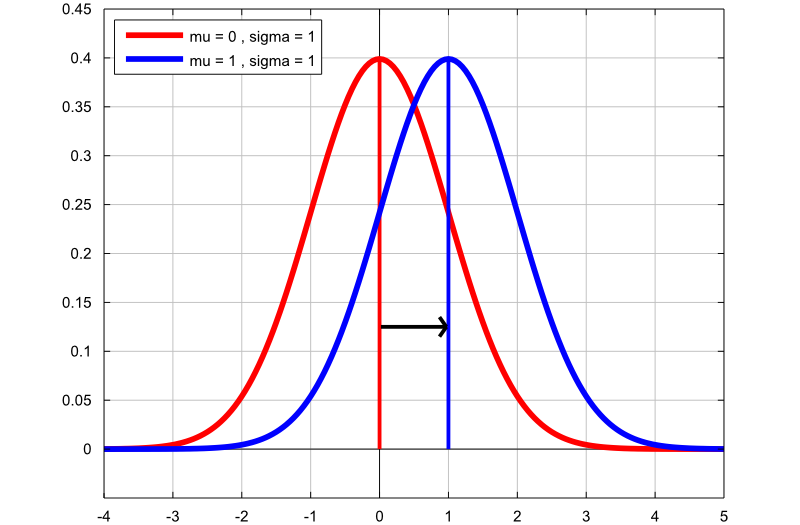
The following plot contains the graphs of two normal probability density functions:

By changing the mean from $mu =0$ to $mu =1$, the shape of the graph does not change, but the graph is translated to the right (its location changes).

Normal density plot 1

Plot 2 - Changing the standard deviation

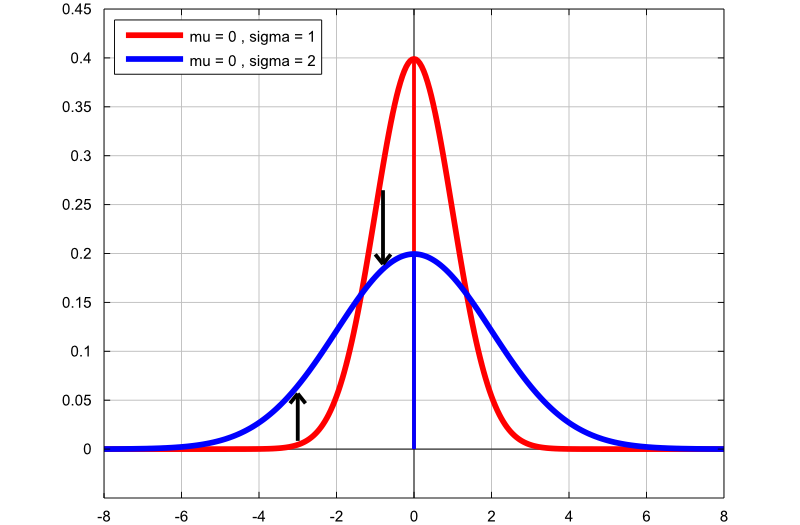
The following plot shows two graphs:

By increasing the standard deviation from $sigma =1$ to $sigma =2$, the location of the graph does not change (it remains centered at 0), but the shape of the graph changes (there is less density in the center and more density in the tails).

Normal density plot 2

More details

The following lectures contain more material about the normal distribution.

Normal distribution values

How to tackle the numerical computation of the distribution function

Multivariate normal distribution

A multivariate generalization of the normal distribution, frequently encountered in statistics

Quadratic forms involving normal variables

Discusses the distribution of quadratic forms involving normal random variables

Linear combinations of normal variables

Discusses the important fact that normality is preserved by linear combinations

Solved exercises

Below you can find some exercises with explained solutions.

Exercise 1

Let X be a normal random variable with mean $mu =3$ and variance $sigma ^{2}=4$. Compute the following probability:[eq40]

Solution

First of all, we need to express the above probability in terms of the distribution function of X:[eq41]

Then, we need to express the distribution function of X in terms of the distribution function of a standard normal random variable Z:[eq42]

Therefore, the above probability can be expressed as[eq43]where we have used the fact that [eq44], which has been presented in the lecture entitled Normal distribution values.

Exercise 2

Let X be a random variable having a normal distribution with mean $mu =1$ and variance $sigma ^{2}=16$. Compute the following probability:[eq45]

Solution

We need to use the same technique used in the previous exercise (express the probability in terms of the distribution function of a standard normal random variable):[eq46]where we have found the value [eq47] in a normal distribution table.

Exercise 3

Suppose the random variable X has a normal distribution with mean $mu =1$ and variance $sigma ^{2}=1$. Define the random variable Y as follows:[eq48]Compute the expected value of Y.

Solution

Remember that the moment generating function of X is[eq49]Therefore, using the linearity of the expected value, we obtain[eq50]

How to cite

Please cite as:

Taboga, Marco (2021). "Normal distribution", Lectures on probability theory and mathematical statistics. Kindle Direct Publishing. Online appendix. https://www.statlect.com/probability-distributions/normal-distribution.

The books

Most of the learning materials found on this website are now available in a traditional textbook format.

Featured pages
Explore
Main sections
About
Glossary entries
Share
  • To enhance your privacy,
  • we removed the social buttons,
  • but don't forget to share.