Eigenvectors corresponding to distinct eigenvalues are linearly independent. As a consequence, if all the eigenvalues of a matrix are distinct, then their corresponding eigenvectors span the space of column vectors to which the columns of the matrix belong.
If there are repeated eigenvalues, but they are not defective (i.e., their algebraic multiplicity equals their geometric multiplicity), the same spanning result holds.
However, if there is at least one defective repeated eigenvalue, then the spanning fails.
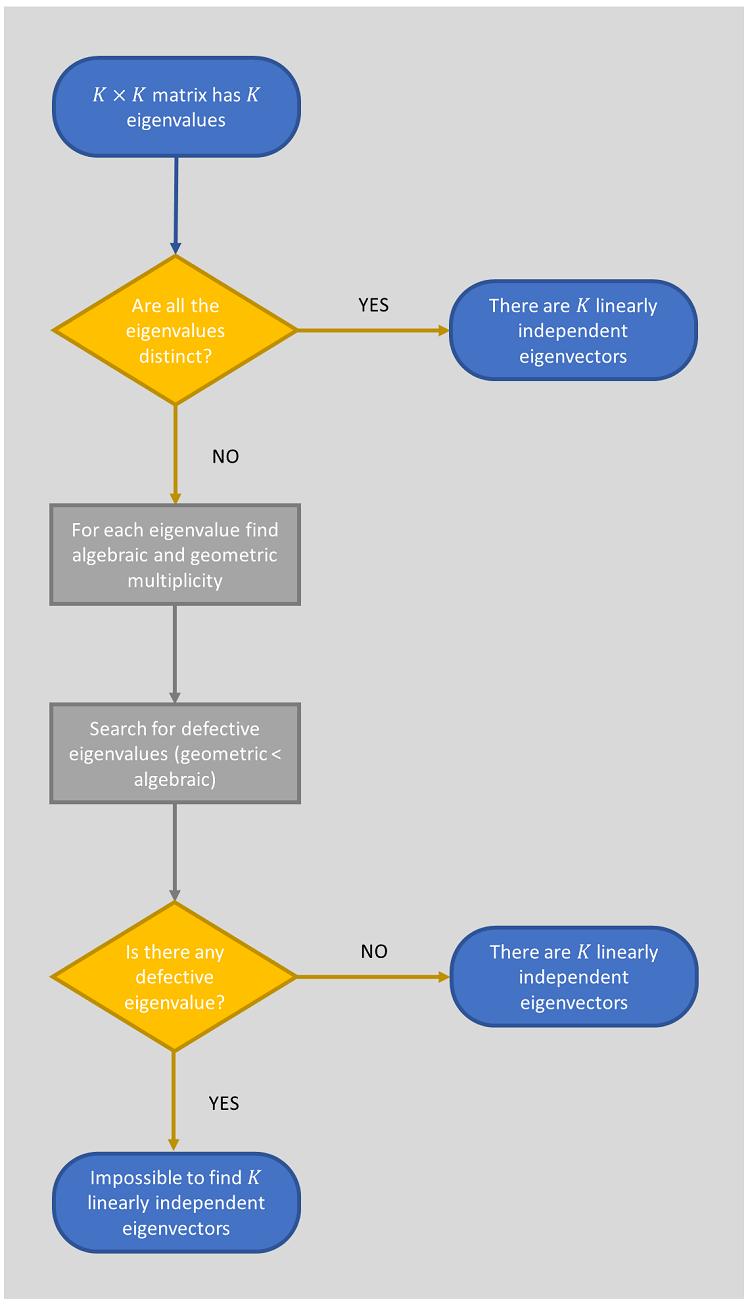
These results will be formally stated, proved and illustrated in detail in the remainder of this lecture.
We now deal with distinct eigenvalues.
Proposition
Let
be a
matrix. Let
(
)
be eigenvalues of
and choose
associated eigenvectors. If there are no repeated eigenvalues (i.e.,
are distinct), then the
eigenvectors
are linearly independent.
The proof is by contradiction. Suppose that
are not linearly independent. Denote by
the largest number of linearly independent eigenvectors. If necessary,
re-number eigenvalues and eigenvectors, so that
are linearly independent. Note that
because a single vector trivially forms by itself a set of linearly
independent vectors. Moreover,
because otherwise
would be linearly independent, a contradiction. Now,
can be written as a linear combination of
:
where
are scalars and they are not all zero (otherwise
would be zero and hence not an eigenvector). By the definition of eigenvalues
and eigenvectors we have
that
and
that
By
subtracting the second equation from the first, we
obtain![]() Since
Since
are distinct,
for
.
Furthermore,
are linearly independent, so that their only linear combination giving the
zero vector has all zero coefficients. As a consequence, it must be that
.
But we have already explained that these coefficients cannot all be zero.
Thus, we have arrived at a contradiction, starting from the initial hypothesis
that
are not linearly independent. Therefore,
must be linearly independent.
When
in the proposition above, then there are
distinct eigenvalues and
linearly independent eigenvectors, which span (i.e., they form a
basis for) the space of
-dimensional
column vectors (to which the columns of
belong).
Example
Define the
matrix
It
has three
eigenvalues
with
associated
eigenvectors
![[eq22]](/images/linear-independence-of-eigenvectors__39.png) which
you can verify by checking that
which
you can verify by checking that
(for
).
The three eigenvalues
,
and
are distinct (no two of them are equal to each other). Therefore, the three
corresponding eigenvectors
,
and
are linearly independent, which you can also verify by checking that none of
them can be written as a linear combination of the other two. These three
eigenvectors form a basis for the space of all
vectors, that is, a
vector
can
be written as a linear combination of the eigenvectors
,
and
for any choice of the entries
,
and
.
We now deal with the case in which some of the eigenvalues are repeated.
Proposition
Let
be a
matrix. If
has some repeated eigenvalues, but they are not defective (i.e., their
geometric
multiplicity equals their algebraic multiplicity), then there exists a set
of
linearly independent eigenvectors of
.
Denote by
the
eigenvalues of
and by
a list of corresponding eigenvectors chosen in such a way that
is linearly independent of
whenever there is a repeated eigenvalue
.
The choice of eigenvectors can be performed in this manner because the
repeated eigenvalues are not defective by assumption. Now, by contradiction,
suppose that
are not linearly independent. Then, there exist scalars
not all equal to zero such
that
Denote
by
the number of distinct eigenvalues. Without loss of generality (i.e., after
re-numbering the eigenvalues if necessary), we can assume that the first
eigenvalues are distinct. For
,
define the sets of indices corresponding to groups of equal
eigenvalues
and
the
vectors
Then,
equation (1)
becomes
Denote
by
the following set of
indices:
The
set
must be non-empty because
are not all equal to zero and the previous choice of linearly independent
eigenvectors corresponding to a repeated eigenvalue implies that the vectors
in equation (2) cannot be made equal to zero by appropriately choosing
positive coefficients
.
Then, we
have
But,
for any
,
is an eigenvector (because
eigenspaces are closed
with respect to linear combinations). This means that a linear combination
(with coefficients all equal to
)
of eigenvectors corresponding to distinct eigenvalues is equal to
.
Hence, those eigenvectors are linearly dependent. But this contradicts the
fact, proved previously, that eigenvectors corresponding to different
eigenvalues are linearly independent. Thus, we have arrived at a
contradiction. Hence, the initial claim that
are not linearly independent must be wrong. As a consequence,
are linearly independent.
Thus, when there are repeated eigenvalues, but none of them is defective, we
can choose
linearly independent eigenvectors, which span the space of
-dimensional
column vectors (to which the columns of
belong).
Example
Define the
matrix
It
has three
eigenvalues
with
associated
eigenvectors
![[eq41]](/images/linear-independence-of-eigenvectors__96.png) which
you can verify by checking that
which
you can verify by checking that
(for
).
The three eigenvalues are not distinct because there is a repeated eigenvalue
whose algebraic multiplicity equals two. However, the two eigenvectors
and
associated to the repeated eigenvalue are linearly independent because they
are not a multiple of each other. As a consequence, also the geometric
multiplicity equals two. Thus, the repeated eigenvalue is not defective.
Therefore, the three eigenvectors
,
and
are linearly independent, which you can also verify by checking that none of
them can be written as a linear combination of the other two. These three
eigenvectors form a basis for the space of all
vectors.
The last proposition concerns defective matrices, that is, matrices that have at least one defective eigenvalue.
Proposition
Let
be a
matrix. If
has at least one defective eigenvalue (whose geometric multiplicity is
strictly less than its algebraic multiplicity), then there does not exist a
set of
linearly independent eigenvectors of
.
Remember that the
geometric
multiplicity of an eigenvalue cannot exceed its algebraic multiplicity. As
a consequence, even if we choose the maximum number of independent
eigenvectors associated to each eigenvalue, we can find at most
of them because there is at least one defective eigenvalue.
Thus, in the unlucky case in which
is a defective matrix, there is no way to form a basis of eigenvectors of
for the space of
-dimensional
column vectors to which the columns of
belong.
Example
Consider the
matrix
The
characteristic polynomial
is
![[eq45]](/images/linear-independence-of-eigenvectors__118.png) and
its roots
are
and
its roots
areThus,
there is a repeated eigenvalue
(
)
with algebraic multiplicity equal to 2. Its associated eigenvectors
solve
the
equation
![[eq49]](/images/linear-independence-of-eigenvectors__122.png) or
orwhich
is satisfied for
and any value of
.
Hence, the eigenspace of
is the linear space that contains
all vectors
of the
form
where
can be any scalar. In other words, the eigenspace of
is generated by a single
vector
Hence,
it has dimension 1 and the geometric multiplicity of
is 1, less than its algebraic multiplicity, which is equal to 2. This implies
that there is no way of forming a basis of eigenvectors of
for the space of two-dimensional column vectors. For example, the
vector
cannot
be written as a multiple of the eigenvector
.
Thus, there is at least one two-dimensional vector that cannot be written as a
linear combination of the
eigenvectors of
.
Below you can find some exercises with explained solutions.
Consider the matrix
Try to find a set of eigenvectors of
that spans the set of all
vectors.
The characteristic polynomial
is![[eq55]](/images/linear-independence-of-eigenvectors__141.png) and
its roots
are
and
its roots
areSince
there are two distinct eigenvalues, we already know that we will be able to
find two linearly independent eigenvectors. Let's find them. The eigenvector
associated
to
solves the
equation
or
which
is satisfied for any couple of values
such that
or
For
example, we can choose
,
so that
and the eigenvector associated to
is
The
eigenvector
associated
to
solves the
equation
or
which
is satisfied for any couple of values
such that
or
For
example, we can choose
,
so that
and the eigenvector associated to
is
Thus,
and
form the basis of eigenvectors we were searching for.
Define
Try to find a set of eigenvectors of
that spans the set of all column vectors having the same dimension as the
columns of
.
The characteristic polynomial
is![[eq70]](/images/linear-independence-of-eigenvectors__170.png) where
in step
where
in step
we have used the
Laplace
expansion along the third row. The roots of the polynomial
are
Hence,
is a repeated eigenvalue with algebraic multiplicity equal to 2. Its
associated eigenvectors
solve
the
equation
![[eq74]](/images/linear-independence-of-eigenvectors__175.png) or
orThis
system of equations is satisfied for any value of
and
.
As a consequence, the eigenspace of
contains all the vectors
that can be written
as
where
the scalar
can be arbitrarily chosen. Thus, the eigenspace of
is generated by a single
vector
Hence,
the eigenspace has dimension
and the geometric multiplicity of
is 1, less than its algebraic multiplicity, which is equal to 2. It follows
that the matrix
is defective and we cannot construct a basis of eigenvectors of
that spans the space of
vectors.
Please cite as:
Taboga, Marco (2021). "Linear independence of eigenvectors", Lectures on matrix algebra. https://www.statlect.com/matrix-algebra/linear-independence-of-eigenvectors.
Most of the learning materials found on this website are now available in a traditional textbook format.