Importance sampling is a variance reduction technique. We use it to reduce the variance of the approximation error that we make when we approximate an expected value with Monte Carlo integration.
In this lecture, we explain how importance sampling works and then we show with an example how effective it can be.
Importance sampling is based on a simple method used to compute expected values in many different but equivalent ways.
The next proposition shows how the technique works for discrete random vectors.
Proposition
Let
be a
discrete random vector with support
and joint probability
mass function
.
Let
be a function
.
Let
be another
discrete random vector
with joint probability mass function
and such that
whenever
.
Then,
![[eq6]](/images/importance-sampling__13.png)
This is obtained as
follows:![[eq7]](/images/importance-sampling__14.png)
An almost identical proposition holds for continuous random vectors.
Proposition
Let
be a continuous
random vector with support
and joint probability
density function
.
Let
be a function
.
Let
be another continuous random vector
with joint probability density function
and such that
whenever
.
Then,
![[eq13]](/images/importance-sampling__26.png)
This is obtained as
follows:![[eq14]](/images/importance-sampling__27.png) where
we have
used
where
we have
usedas
a shorthand for the multiple integral over the coordinates of
.
Suppose that we need to compute the expected
valueof
a function of a random vector
by Monte Carlo integration.
The standard way to proceed is to produce a computer-generated sample of
realizations of
independent random vectors
,...,
having the same distribution as
.
Then, we use the sample mean
to
approximate the expected value.
Thanks to the propositions in the previous section, we can compute an
alternative Monte Carlo approximation of
by extracting
independent draws
from the distribution of another random vector
(in what follows we assume that it is discrete, but everything we say applies
also to continuous vectors).
Then, we use the sample
meanas
an approximation.
This technique is called importance sampling.
The reason why we use importance sampling is that we can often choose
in such a way that the variance of the approximation error is much smaller
than the variance of the standard Monte Carlo approximation.
In the case of the standard Monte Carlo approximation, the variance of the
approximation error
is
In the case of importance sampling, the variance of the approximation error
is
In the standard case, the approximation
error
isand
its variance
is
![[eq24]](/images/importance-sampling__46.png) In
the case of importance sampling, we
have
In
the case of importance sampling, we
have![[eq25]](/images/importance-sampling__47.png)
Ideally, we would like to be able to choose
in such a way that
is
a constant, which would imply that the variance of the approximation error is
zero.
The next proposition shows when this ideal situation is achievable.
Proposition
If
for any
,
then
when
has joint probability mass
function
![[eq29]](/images/importance-sampling__54.png)
The ratio
is
constant if the proportionality
condition
holds.
By imposing that
be a legitimate probability density function, we
get
or
Of course, the denominator
is unknown (otherwise we would not be discussing how to compute a Monte Carlo
approximation for it), so that it is not feasible to achieve the optimal
choice for
.
However, the formula for the probability mass function (pmf) of the optimal
gives us some indications about the choice of
.
In particular, equation (1) tells us that the pmf of
should place more mass where the product between the pmf of
and the value of
is larger.
This product is a measure of the importance of the possible
values of
.
Therefore, the pmf of
should be tilted so as to give more weight to the more important values of
.
Before showing an example, let us summarize the main takeaways from this lecture:
importance sampling is a way of computing a Monte Carlo approximation of
;
we extract
independent draws
from a distribution that is different from that of
we use the weighted sample
meanas
an approximation of
;
this approximation has small variance when the pmf of
puts more mass than the pmf of
on the important points;
the important points are those for which
is larger; they give a "substantial contribution" to the expected value;
when we average our samples, we take into account the fact that we
over-sampled the important points by weighting them down with the
weights
which
are smaller than
when
is larger than
.
Let us now illustrate importance sampling with an example.
Suppose that
has a standard
normal distribution (i.e., with mean
and standard deviation
)
and
![]()
The function
attains its maximum at the point
and then rapidly goes to
for values of
that are smaller or larger than
.
On the contrary, the probability density function
of a standard normal random variable is almost zero at
.
As a consequence, if we use a standard Monte Carlo approximation:
we extract lots of values of
for which
is almost zero;
we extract very few values for which
is different from zero.
This results in a high variance of the approximation error.
In order to shift weight towards
,
we can sample
from a normal distribution with mean
and standard deviation
.
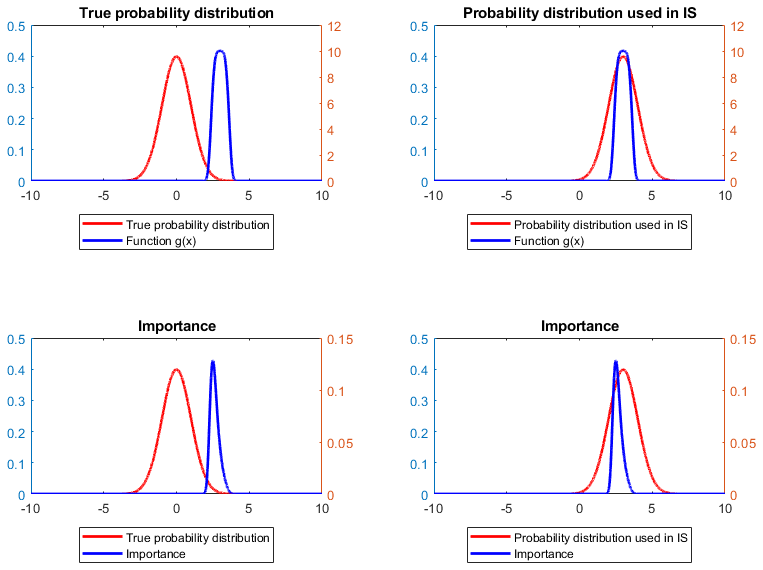
The following Python code shows how to do so and computes the standard Monte
Carlo (MC) and the importance sampling
(IS) approximations by using samples of
independent draws from the distributions of
and
.
The standard deviations of the two approximations
(std_MC and std_IS) are
estimated by using the sample
variances of
and
.
If you run this example code, you can see that indeed the importance sampling approximation achieves a significant reduction in the approximation error (from 0.0080 to 0.0012).
# Example of importance sampling in Python
import numpy as np
from scipy.stats import norm
n = 10000 # Number of Monte Carlo samples
np.random.seed(0) # Initialization of random number generator for replicability
# Standard Monte Carlo
x = np.random.randn(n, 1)
g = 10 * np.exp(-5 * (x - 3) ** 4)
MC = np.mean(g)
std_MC = np.sqrt(( 1 / n) * np.var(g))
print('Standard Monte-Carlo estimate of the expected value: ' + str(MC))
print('Standard deviation of plain-vanilla Monte Carlo: ' + str(std_MC))
print(' ')
# Importance sampling
y = 3 + np.random.randn(n, 1);
g = 10 * np.exp(-5 * (y - 3) ** 4);
g_weighted = g * norm.pdf(y, 0, 1) / norm.pdf(y, 3, 1);
IS = np.mean(g_weighted)
std_IS = np.sqrt((1 / n) * np.var(g_weighted))
print('Importance-sampling Monte-Carlo estimate of the expected value: ' + str(IS))
print('Standard deviation of importance-sampling Monte Carlo: ' + str(std_IS))The output is:
Standard Monte-Carlo estimate of the expected value: 0.08579415409780462
Standard deviation of plain-vanilla Monte Carlo: 0.007904811247115087
Importance-sampling Monte-Carlo estimate of the expected value: 0.09096069224808337
Standard deviation of importance-sampling Monte Carlo: 0.0011925073695279826Please cite as:
Taboga, Marco (2021). "Importance sampling", Lectures on probability theory and mathematical statistics. Kindle Direct Publishing. Online appendix. https://www.statlect.com/asymptotic-theory/importance-sampling.
Most of the learning materials found on this website are now available in a traditional textbook format.