The joint distribution function is a function that completely characterizes the probability distribution of a random vector.
Table of contents
It is also called joint cumulative distribution function (abbreviated as joint cdf).
Let us start with the simple case in which we have two random variables
and
.
Their joint cdf is defined
aswhere
and
are two real numbers.
Note that:
indicates a
probability;
the comma inside the parentheses stands for AND.
In other words, the joint cdf
gives the probability that two conditions are simultaneously true:
the random variable
takes a value less than or equal to
;
the random variable
takes a value less than or equal to
.
Suppose that there are only four possible
cases:
Further assume that each of these cases has probability equal to 1/4.
Let us compute, as an example, the following value of the joint distribution
function:
The two conditions that need to be simultaneously true
are:
There are two cases in which they are
satisfied:
Therefore, we
have![[eq7]](/images/joint-distribution-function__16.png)
In the previous example we have shown a special case.
In general, the formula for the joint cdf of two discrete random variables
and
is:![[eq8]](/images/joint-distribution-function__19.png)
where:
is the support of the
vector
,
that is, the set of all the values of
that have a strictly positive probability of being observed;
we sum the probabilities over the
setthat
contains all the couples
belonging to the support and such that
and
.
The probabilities in the sum are often written using the so-called
joint probability mass
function
The sum in the formula above can be easily computed with the help of a table.
Here is an example.
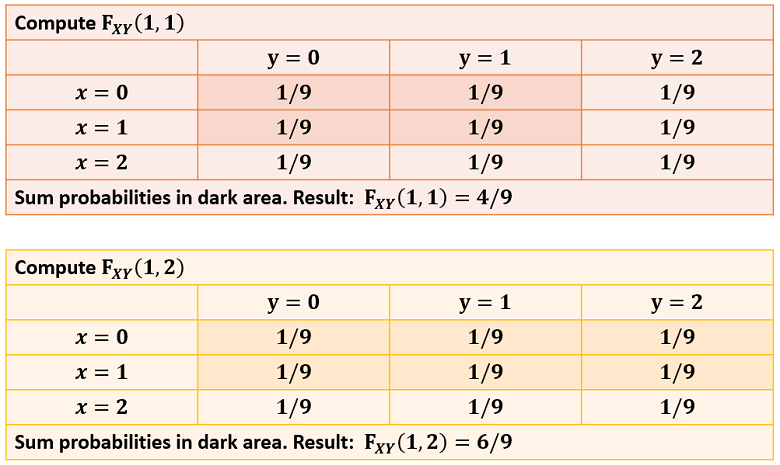
In this table, there are nine possible couples
and they all have the same probability (1/9).
In order to compute the joint cumulative distribution function, all we need to
do is to shade all the probabilities to the left of
(included) and above
(included).
Then, the value of
is equal to the sum of the probabilities in the shaded area.
When
and
are continuous
random variables, we need to use the
formula![[eq14]](/images/joint-distribution-function__34.png){kind=small}
where
is the joint
probability density function of
and
.
The computation of the double integral can be broken down in two steps:
first compute the inner
integralwhich,
in general, is a function of
and
;
then calculate the outer
integral
Let us make an example.
Let the joint pdf
be![[eq17]](/images/joint-distribution-function__42.png)
When
and
,
we have
![[eq20]](/images/joint-distribution-function__45.png)
This is only one of the possible cases. We also have the two cases:
or
,
in which
case
and
,
in which
case![[eq22]](/images/joint-distribution-function__51.png)
The two marginal
distribution functions of
and
are
They can be derived from the joint cumulative distribution function as
follows:where
the exact meaning of the notation
is
This can be demonstrated as
follows:![[eq26]](/images/joint-distribution-function__57.png){kind=small}
because
the condition
is always met and, as a consequence, the condition
is
satisfied whenever
is true.
The proof for
is analogous.
In general, we cannot derive the joint cdf from the marginals, unless we know the so-called copula function, which links the two marginals.
However, there is an important exception, discussed in the next section.
When
and
are independent, then the joint cdf is equal to the product of the
marginals:
See the lecture on independent random variables for a proof, a discussion and some examples.
Until now, we have discussed the case of two random variables. However, the joint cdf is defined for any collection of random variables forming a random vector.
Definition
The joint distribution function of a
random vector
is a function
such
that:![[eq30]](/images/joint-distribution-function__68.png){kind=small}
where
the entries of
and
are denoted by
and
respectively, for
.
More details about joint distribution functions can be found in the lecture entitled Random vectors.
Previous entry: Integrable random variable
Next entry: Joint probability density function
Please cite as:
Taboga, Marco (2021). "Joint distribution function", Lectures on probability theory and mathematical statistics. Kindle Direct Publishing. Online appendix. https://www.statlect.com/glossary/joint-distribution-function.
Most of the learning materials found on this website are now available in a traditional textbook format.
